33. Recursion
A child couldn't sleep, so her mother told her a story about a little frog,
who couldn't sleep, so the frog's mother told her a story about a little bear,
who couldn't sleep, so the bear's mother told her a story about a little weasel...
who fell asleep.
...and the little bear fell asleep;
...and the little frog fell asleep;
...and the child fell asleep.
(Source: http://everything2.com/title/recursion)
Recursion is an object or process that is defined in terms of itself. Mathematical patterns such as factorials and the Fibonacci series are recursive. Documents that can contain other documents, which themselves can contain other documents, are recursive. Fractal images, and even certain biological processes are recursive in how they work.
33.1. Where is Recursion Used?
Documents, such as web pages, are naturally recursive. For example, Figure 20.1 shows a simple web document.
Figure 20.1: Web page
That web document can be contained in a „box,“ which can help layout the page as shown in Figure 20.2.
Figure 20.2: Web page with tables
This works recursively. Each box can contain a web page, that can have a box, which could contain another web page as shown in Figure 20.3.
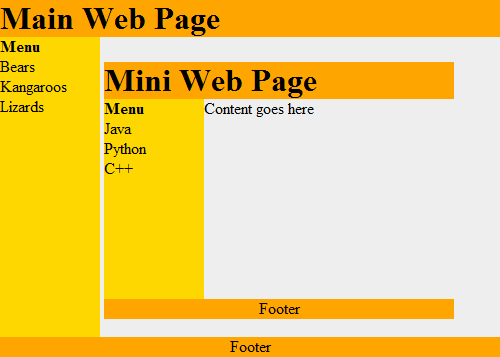
Figure 20.3: Web page with recursion
Recursive functions are often used with advanced searching and sorting algorithms. We’ll show some of that here and if you take a „data structures“ class you will see a lot more of it.
Even if a person does not become a programmer, understanding the concept of recursive systems is important. If there is a business need for recursive table structures, documents, or something else, it is important to know how to specify this to the programmer up front.
For example, a person might specify that a web program for recipes needs the ability to support ingredients and directions. A person familiar with recursion might state that each ingredient could itself be a recipes with other ingredients (that could be recipes.) The second system is considerably more powerful.
33.2. How is Recursion Coded?
In prior chapters, we have used functions that call other functions. For example:
1 2 3 4 5 6 7 8 | def f(): g() print("f") def g(): print("g") f() |
It is also possible for a function to call itself. A function that calls itself is using a concept called recursion. For example:
1 2 3 4 5 | def f(): print("Hello") f() f() |
The example above will print Hello and then call the f() function
again. Which will cause another Hello to be printed out and another call
to the f() function. This will continue until the computer runs out
of something called stack space. When this happens, Python will output a
long error that ends with:
RuntimeError: maximum recursion depth exceeded
The computer is telling you, the programmer, that you have gone too far down the rabbit hole.
33.3. Controlling Recursion Depth
To successfully use recursion, there needs to be a way to prevent the function from endlessly calling itself over and over again. The example below counts how many times it has been called, and uses an if statement to exit once the function has called itself ten times.
1 2 3 4 5 6 7 8 9 10 11 | def f(level): # Print the level we are at print("Recursion call, level",level) # If we haven't reached level ten... if level < 10: # Call this function again # and add one to the level f(level+1) # Start the recursive calls at level 1 f(1) |
1 2 3 4 5 6 7 8 9 10 | Recursion call, level 1 Recursion call, level 2 Recursion call, level 3 Recursion call, level 4 Recursion call, level 5 Recursion call, level 6 Recursion call, level 7 Recursion call, level 8 Recursion call, level 9 Recursion call, level 10 |
33.4. Recursion In Mathematics
33.4.1. Recursion Factorial Calculation
Any code that can be done recursively can be done without using recursion. Some programmers feel that the recursive code is easier to understand.
Calculating the factorial of a number is a classic example of using recursion. Factorials are useful in probability and statistics. For example:
Recursively, this can be described as:
Below are two example functions that calculate . The first one is non-recursive, the second is recursive.
1 2 3 4 5 6 7 | # This program calculates a factorial # WITHOUT using recursion def factorial_nonrecursive(n): answer = 1 for i in range(2, n + 1): answer = answer * i return answer |
1 2 3 4 5 6 7 | # This program calculates a factorial # WITH recursion def factorial_recursive(n): if n == 1: return 1 elif n > 1: return n * factorial_recursive(n - 1) |
The functions do nothing by themselves. Below is an example where we put it all together. This example also adds some print statements inside the function so we can see what is happening.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | # This program calculates a factorial # WITHOUT using recursion def factorial_nonrecursive(n): answer = 1 for i in range(2, n + 1): print(i, "*", answer, "=", i * answer) answer = answer * i return answer print("I can calculate a factorial!") user_input = input("Enter a number:") n = int(user_input) answer = factorial_nonrecursive(n) print(answer) # This program calculates a factorial # WITH recursion def factorial_recursive(n): if n == 1: return 1 else: x = factorial_recursive(n - 1) print( n, "*", x, "=", n * x ) return n * x print("I can calculate a factorial!") user_input = input("Enter a number:") n = int(user_input) answer = factorial_recursive(n) print(answer) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | I can calculate a factorial! Enter a number:7 2 * 1 = 2 3 * 2 = 6 4 * 6 = 24 5 * 24 = 120 6 * 120 = 720 7 * 720 = 5040 5040 I can calculate a factorial! Enter a number:7 2 * 1 = 2 3 * 2 = 6 4 * 6 = 24 5 * 24 = 120 6 * 120 = 720 7 * 720 = 5040 5040 |
33.4.2. Recursive Expressions
Say you have a mathematical expression like this:
\(f_{n} = \begin{cases} 6 & \text{if } n = 1, \\ \frac{1}{2}f_{n-1}+4 & \text{if } n > 1. \end{cases}\)
Looks complicated, but it just means that if \(n=1\) we are working with \(f_{1}\). That function returns a 6.
For \(f_{2}\) we return \(\frac{1}{2}f_{1}+4\).
The code would start with:
1 | def f(n): |
Then we need to add that first case:
1 2 3 | def f(n): if n == 1: return 6 |
See how closely if follows the mathematical notation? Now for the rest:
1 2 3 4 5 | def f(n): if n == 1: return 6 elif n > 1: return (1 / 2) * f(n - 1) + 4 |
Converting these types of mathematical expressions to code is straight forward. But we’d better try it out in a full example:
1 2 3 4 5 6 7 8 9 10 11 12 13 | def f(n): if n == 1: return 6 elif n > 1: return (1 / 2) * f(n - 1) + 4 def main(): result = f(10) print(result) main() |
33.5. Recursive Graphics
33.5.1. Recursive Rectangles
Recursion is great to work with structured documents that are themselves recursive. For example, a web document can have a table divided into rows and columns to help with layout. One row might be the header, another row the main body, and finally the footer. Inside a table cell, might be another table. And inside of that can exist yet another table.
Another example is e-mail. It is possible to attach another person’s e-mail to a your own e-mail. But that e-mail could have another e-mail attached to it, and so on.
Can we visually see recursion in action in one of our Pygame programs? Yes! Figure 19.4 shows an example program that draws a rectangle, and recursively keeps drawing rectangles inside of it. Each rectangle is 20% smaller than the parent rectangle. Look at the code. Pay close attention to the recursive call in the recursive_draw function.
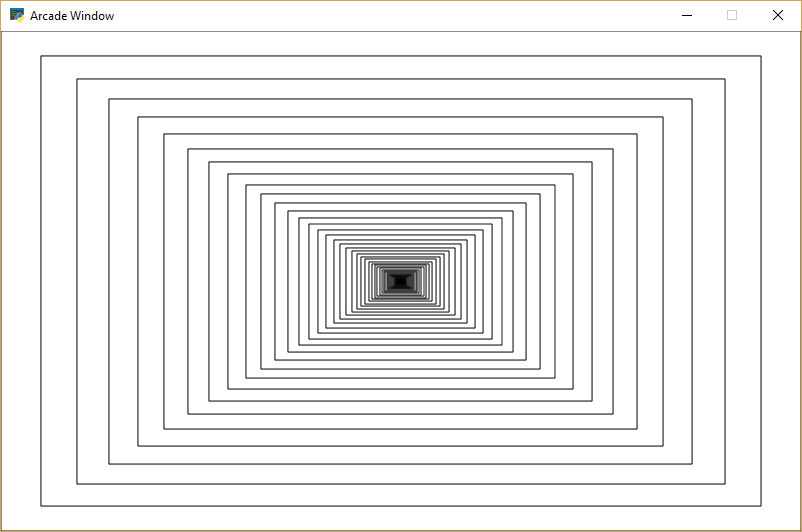
Figure 20.4: Recursive Rectangles
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | """ Recursive Rectangles """ import arcade SCREEN_WIDTH = 800 SCREEN_HEIGHT = 500 def draw_rectangle(x, y, width, height): """ Recursively draw a rectangle, each one a percentage smaller """ # Draw it arcade.draw_rectangle_outline(x, y, width, height, arcade.color.BLACK) # As long as we have a width bigger than 1, recursively call this function with a smaller rectangle if width > 1: # Draw the rectangle 90% of our current size draw_rectangle(x, y, width * .9, height * .9) class MyWindow(arcade.Window): """ Main application class. """ def __init__(self, width, height): super().__init__(width, height) arcade.set_background_color(arcade.color.WHITE) def on_draw(self): """ Render the screen. """ arcade.start_render() # Find the center of our screen center_x = SCREEN_WIDTH / 2 center_y = SCREEN_HEIGHT / 2 # Start our recursive calls draw_rectangle(center_x, center_y, SCREEN_WIDTH, SCREEN_HEIGHT) def main(): MyWindow(SCREEN_WIDTH, SCREEN_HEIGHT) arcade.run() if __name__ == "__main__": main() |
33.5.2. Fractals
Fractals are defined recursively. Here is a very simple fractal, showing how it changes depending on how „deep“ the recursion goes.

Figure 20.5: Recursive Fractal Level 0
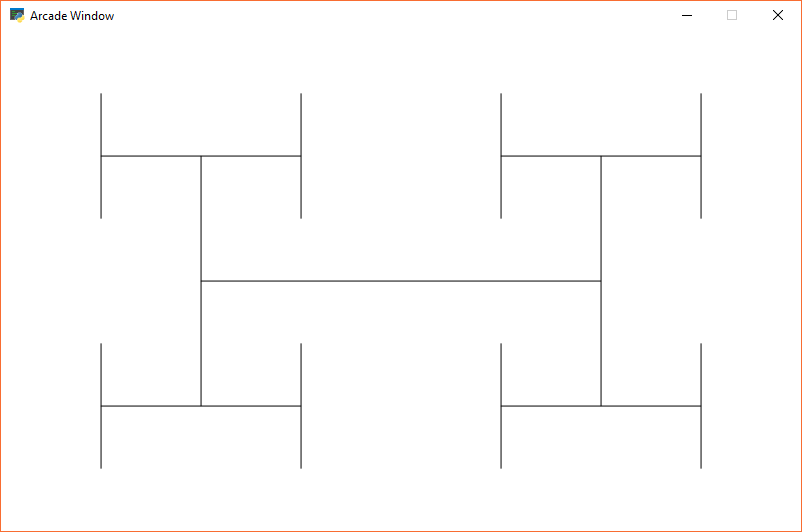
Figure 20.6: Recursive Fractal Level 1
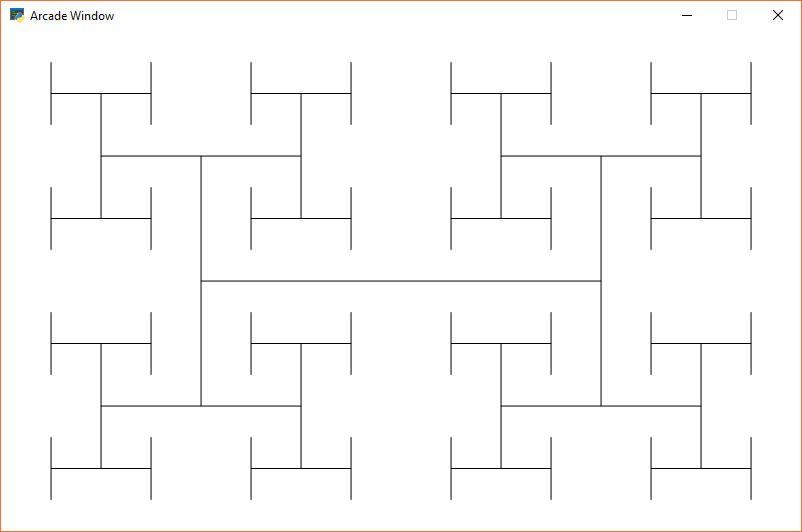
Figure 20.7: Recursive Fractal Level 2

Figure 20.8: Recursive Fractal Level 5
Here is the source code for the „H“ fractal:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | """ Recursive H's """ import arcade SCREEN_WIDTH = 800 SCREEN_HEIGHT = 500 RECURSION_DEPTH = 0 def draw_h(x, y, width, height, count): """ Recursively draw an H, each one a half as big """ # Draw the H # Draw cross-bar arcade.draw_line(x + width * .25, height / 2 + y, x + width * .75, height / 2 + y, arcade.color.BLACK) # Draw left side arcade.draw_line(x + width * .25, height * .5 / 2 + y, x + width * .25, height * 1.5 / 2 + y, arcade.color.BLACK) # Draw right side arcade.draw_line(x + width * .75, height * .5 / 2 + y, x + width * .75, height * 1.5 / 2 + y, arcade.color.BLACK) # As long as we have a width bigger than 1, recursively call this function with a smaller rectangle if count > 0: count -= 1 # Draw the rectangle 90% of our current size # Draw lower left draw_h(x, y, width / 2, height / 2, count) # Draw lower right draw_h(x + width / 2, y, width / 2, height / 2, count) # Draw upper left draw_h(x, y + height / 2, width / 2, height / 2, count) # Draw upper right draw_h(x + width / 2, y + height / 2, width / 2, height / 2, count) class MyWindow(arcade.Window): """ Main application class. """ def __init__(self, width, height): super().__init__(width, height) arcade.set_background_color(arcade.color.WHITE) def on_draw(self): """ Render the screen. """ arcade.start_render() # Start our recursive calls draw_h(0, 0, SCREEN_WIDTH, SCREEN_HEIGHT, RECURSION_DEPTH) def main(): MyWindow(SCREEN_WIDTH, SCREEN_HEIGHT) arcade.run() if __name__ == "__main__": main() |
You can explore fractals on-line:
If you want to program your own fractals, you can get ideas of easy fractals by looking at Chapter 8 of The Nature of Code by Daniel Shiffman.
33.6. Recursive Mazes
There are maze generation algorithms. Wikipedia has a nice Maze generation algorithm article that details some. One way is the recursive division method.
The algorithm is described below. Images are from Wikipedia.
Begin with the maze’s space with just the outside walls. Call this a chamber.
Divide the chamber with one random horizontal wall, and one random vertical wall.
Pick three of the four walls and put a randomly position opening in it.
Subdivide each of the four sections. Call each a chamber. Recursively call this function. In this image, the top right chamber has been subdivided.
Finished maze.
This method results in mazes with long straight walls crossing their space, making it easier to see which areas to avoid.

Recursive maze generation. Source: Wikipedia Maze generation algorithm.
Here is sample Python code that creates a maze using this method:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 | import random # These constants are used to determine what should be stored in the grid if we have an empty # space or a filled space. EMPTY = " " WALL = "XXX" # Maze must have an ODD number of rows and columns. # Walls go on EVEN rows/columns. # Openings go on ODD rows/columns MAZE_HEIGHT = 51 MAZE_WIDTH = 51 def create_grid(width, height): """ Create an empty grid. """ grid = [] for row in range(height): grid.append([]) for column in range(width): grid[row].append(EMPTY) return grid def print_maze(maze): """ Print the maze. """ # Loop each row, but do it in reverse so 0 is at the bottom like we expect for row in range(len(maze) - 1, -1, -1): # Print the row/y number print(f"{row:3} - ", end="") # Loop the row and print the content for column in range(len(maze[row])): print(f"{maze[row][column]}", end="") # Go down a line print() # Print the column/x at the bottom print(" ", end="") for column in range(len(maze[0])): print(f"{column:3}", end="") print() def create_outside_walls(maze): """ Create outside border walls.""" # Create left and right walls for row in range(len(maze)): maze[row][0] = WALL maze[row][len(maze[row])-1] = WALL # Create top and bottom walls for column in range(1, len(maze[0]) - 1): maze[0][column] = WALL maze[len(maze[0]) - 1][column] = WALL def create_maze(maze, top, bottom, left, right): """ Recursive function to divide up the maze in four sections and create three gaps. Walls can only go on even numbered rows/columns. Gaps can only go on odd numbered rows/columns. Maze must have an ODD number of rows and columns. """ # Figure out where to divide horizontally start_range = bottom + 2 end_range = top - 1 y = random.randrange(start_range, end_range, 2) # Do the division for column in range(left + 1, right): maze[y][column] = WALL # Figure out where to divide vertically start_range = left + 2 end_range = right - 1 x = random.randrange(start_range, end_range, 2) # Do the division for row in range(bottom + 1, top): maze[row][x] = WALL # Now we'll make a gap on 3 of the 4 walls. # Figure out which wall does NOT get a gap. wall = random.randrange(4) if wall != 0: gap = random.randrange(left + 1, x, 2) maze[y][gap] = EMPTY if wall != 1: gap = random.randrange(x + 1, right, 2) maze[y][gap] = EMPTY if wall != 2: gap = random.randrange(bottom + 1, y, 2) maze[gap][x] = EMPTY if wall != 3: gap = random.randrange(y + 1, top, 2) maze[gap][x] = EMPTY # Print what's going on print(f"Top/Bottom: {top}, {bottom} Left/Right: {left}, {right} Divide: {x}, {y}") print_maze(maze) print() # If there's enough space, to a recursive call. if top > y + 3 and x > left + 3: create_maze(maze, top, y, left, x) if top > y + 3 and x + 3 < right: create_maze(maze, top, y, x, right) if bottom + 3 < y and x + 3 < right: create_maze(maze, y, bottom, x, right) if bottom + 3 < y and x > left + 3: create_maze(maze, y, bottom, left, x) def main(): # Create the blank grid maze = create_grid(MAZE_WIDTH, MAZE_HEIGHT) # Fill in the outside walls create_outside_walls(maze) # Start the recursive process create_maze(maze, MAZE_HEIGHT - 1, 0, 0, MAZE_WIDTH - 1) if __name__ == "__main__": main() |
33.7. Recursive Binary Search
Recursion can be also be used to perform a binary search. Here is a non-recursive binary search from Chapter 15:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def binary_search_nonrecursive(search_list, key): lower_bound = 0 upper_bound = len(search_list) - 1 found = False while lower_bound < upper_bound and found == False: middle_pos = (lower_bound + upper_bound) // 2 if search_list[middle_pos] < key: lower_bound = middle_pos + 1 elif search_list[middle_pos] > key: upper_bound = middle_pos else: found = True if found: print( "The name is at position",middle_pos) else: print( "The name was not in the list." ) binary_search_nonrecursive(name_list,"Morgiana the Shrew") |
This same binary search written in a recursive manner:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | def binary_search_recursive(search_list, key, lower_bound, upper_bound): middle_pos = (lower_bound + upper_bound) // 2 if search_list[middle_pos] < key: # Recursively search top half binary_search_recursive(search_list, key, middle_pos + 1, upper_bound) elif search_list[middle_pos] > key: # Recursively search bottom half binary_search_recursive(search_list, key, lower_bound, middle_pos ) else: print("Found at position", middle_pos) lower_bound = 0 upper_bound = len(name_list) - 1 binary_search_recursive(name_list, "Morgiana the Shrew", lower_bound, upper_bound) |